플로이드 와샬(Floyd-Warshall)
플로이드 와샬 알고리즘은 모든 정점에서 모든 정점까지의 최소비용(최단거리)을 구할 수 있는 알고리즘이다.
이차원배열을 이용하여 풀고 DP를 기반으로 한 알고리즘이다.
플로이드 와샬 알고리즘은 직통으로 가는 비용과 하나의 정점을 경유하였을 때의 비용 중 최소 비용을 구하여 그래프에 계속 갱신해주는 것을 말한다.
A에서 C정점을 갈 때 직통으로 가는 비용과
A에서 B정점을 경유하여 C로 가는 비용을 비교하여 더 낮은 비용을 갱신해주는 것이다.
설명

왼쪽과 같은 그래프가 주어졌을 때 오른쪽과 같은 이차원배열이 만들어질 것이다.
graph[i][j] = i정점에서 j정점으로 이동하는 최소 비용
(이동할 수 없는 경우 inf:무한을 입력해준다.
자기자신으로 이동하는 경우는 없기때문에 i와 j가 같은경우 0을 넣어준다.)
다음으로 아까 정의했던 '직통 비용과 하나의 정점을 경유했을 때 비용 중 최소비용을 구한다' 라는 개념을 사용한다.
1번 정점을 경유하는 경우를 구해보면
2 -> 1 -> 3 : 직통 graph[2][3] 과 graph[2][1] + graph[1][3] 중에 최소비용
2 -> 1 -> 4 : 직통 graph[2][4] 과 graph[2][1] + graph[1][4] 중에 최소비용
3 -> 1 -> 2 / 3 -> 1 -> 4 / 4 -> 1 -> 2 / 4 -> 1 ->3 도 마찬가지로 구해준다.
여기까지 구하면 그래프는 다음과 같이 완성된다.
(주황색 부분이 비용을 계산하여 비교한 부분이고 하얗게 써진 부분이 최소비용이 갱신된 부분이다.)

다음으로 2번 정점을 경유하는 경우를 구해준다.
1 -> 2 -> 3 : 직통 graph[1][3] 과 graph[1][2] + graph[2][3] 중에 최소비용
1 -> 2 -> 4 : 직통 graph[1][4] 과 graph[1][2] + graph[2][4] 중에 최소비용
...나머지도 마찬가지로 구해준다.
그래프는 다음과 같이 완성된다.

3번 정점을 경유하는 경우를 구하면

마지막으로 4번 정점을 경유하는 경우를 구하면 완성이다!
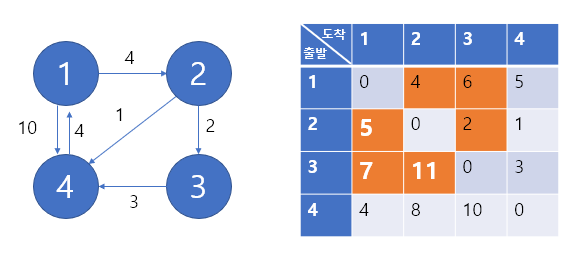
이렇게해서 각 정점에서 모든 다른 정점으로 이동하는 최소비용을 구할 수 있다.
구현
int N = 4; // 정점의 수
int[][] graph = new int[N][N];
for (int i = 0; i < N; i++) { // 경유하는 정점
for (int j = 0; j < N; j++) { // 출발 정점
for (int k = 0; k < N; k++) { // 도착 정점
// 합연산에서 오류가 날 수 있기때문에 무한값을 만나면 넘어간다
if (graph[j][i] == Integer.MAX_VALUE || graph[i][k] == Integer.MAX_VALUE) continue;
// 직통비용과 경유비용 중 최소비용으로 갱신
graph[j][k] = Math.min(graph[i][j], graph[j][i] + graph[i][k]);
}
}
}
주의점
그래프에 음수 사이클이 없어야한다.
(비용이 음수인 것은 상관없다.)
*음수사이클 : 사이클의 모든 경로를 지나 원점으로 돌아왔을 때 결과 비용이 음수가 되는 경우
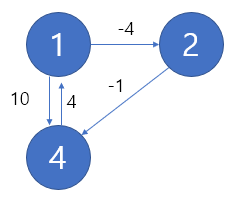
1->2->4 : 최소비용 = -1
이처럼 음수사이클이 생기게되면 최소값을 갱신하는 부분에서 문제가 생기기때문에 불가능하다.
시간 복잡도
코드에서 볼 수 있듯이 3중 for문을 사용한다.
따라서 O(N³)의 시간복잡도를 가진다.
정점 100개일 때 100만
300개일 때 2700만
500개일 때 1억2500만...
정점의 개수가 적을 때만 사용가능하다.
활용 문제
11403번: 경로 찾기
가중치 없는 방향 그래프 G가 주어졌을 때, 모든 정점 (i, j)에 대해서, i에서 j로 가는 경로가 있는지 없는지 구하는 프로그램을 작성하시오.
www.acmicpc.net
비용은 생각하지 않고 플로이드와샬 알고리즘을 활용하여 이동이 가능하면 1을 불가능하면 0을 그래프에 넣어주면 된다.
11404번: 플로이드
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net
전형적인 플로이드와샬 알고리즘 문제이다. 위에서 학습한 그대로 작성하면 풀 수 있었다.
[ 알고리즘과 문법을 공부한 내용을 정리해보는 공간입니다. 부족한 부분이나 잘못된 부분 지적해주시면 감사하겠습니다.]
'공부 일지 > 알고리즘' 카테고리의 다른 글
| [알고리즘] LCA (0) | 2023.02.14 |
|---|---|
| [알고리즘] 플로이드(Floyd) 알고리즘 (0) | 2023.02.06 |
| [알고리즘] 최소 신장 트리(MST) - 프림, 크루스칼 알고리즘 (0) | 2023.02.02 |
| [알고리즘] 위상정렬(Topological Sorting) (0) | 2023.01.28 |
| [알고리즘] 문자열 알고리즘 - KMP알고리즘 (0) | 2023.01.18 |


